Welcome to the start of your Class 12 Physics journey! It all begins with Chapter 1: Electric Charges and Fields. Getting a good handle on these core ideas is the key to feeling confident and acing your board exams later on.
To make sure you get off to a great start, we’ve brought together everything you need in one easy-to-find place. Here you’ll find quick notes for revision, detailed solutions to every NCERT problem, a handpicked list of important multiple-choice questions, solved examples from past exams, and the key derivations explained simply.
Let’s dive in and build a rock-solid foundation in electrostatics together!
Quick Revision Guide on Electric Charges and Fields
1. Electric Charge
- Types: Positive and Negative.
- Basic Property: Like charges repel, unlike charges attract.
- Quantisation: Charge is quantized; any charge
 is an integral multiple of the fundamental charge
is an integral multiple of the fundamental charge  .
. , where
, where  and
and  .
. - Conservation: The total charge in an isolated system remains constant.
- Additivity: The total charge of a system is the algebraic sum of all individual charges.
2. Coulomb’s Law
The electrostatic force between two point charges ![]() and
and ![]() separated by distance
separated by distance ![]() is:
is:
- Magnitude:

- Vector Form:

- Constant:

3. Electric Field
- Definition: Force per unit positive test charge.

- Field due to a point charge
 :
: 
- Superposition Principle: The net electric field at a point is the vector sum of fields due to all individual charges.

4. Electric Dipole
- A pair of equal and opposite charges (
 and
and  ) separated by a small distance
) separated by a small distance  .
. - Dipole Moment
 :
:  (Direction: from
(Direction: from  to
to  ).
). - Field on Axial Line:
 (for
(for  )
) - Field on Equatorial Line:
 (for
(for  )
) - Torque in a Uniform Field (
 ):
):  ; Magnitude:
; Magnitude: 
5. Electric Flux
- Definition: Measure of the flow of the electric field through a given area.

- For a closed surface:

6. Gauss’s Law
- The net flux through a closed surface is
 times the net charge enclosed by the surface.
times the net charge enclosed by the surface.
- Key Applications:
- Infinite Long Wire:

- Infinite Plane Sheet:

- Thin Spherical Shell:
- Outside (
 ):
): 
- Inside (
 ):
): 
- Outside (
7. Continuous Charge Distribution
- Linear Charge Density (
 ):
): 
- Surface Charge Density (
 ):
): 
- Volume Charge Density (
 ):
): 
Quick Revision Tip:
Focus on the formulas for the electric field of a point charge, a dipole (axial and equatorial), and the three standard applications of Gauss’s Law (wire, sheet, shell). Remember that Gauss’s Law is most useful for symmetric charge distributions.
Chapter‑End Questions: Fully Worked Solutions
Exercise 1.1
Question: What is the force between two small charged spheres having charges of ![]() and
and ![]() placed 30 cm apart in air?
placed 30 cm apart in air?
Solution:
- Use Coulomb’s Law:

- Substitute values:
 ,
,  ,
,  ,
, 
- Calculate:




Answer: ![]() (repulsive)
(repulsive)
Exercise 1.2
Question: The electrostatic force on a small sphere of charge 0.4 ![]() C due to another small sphere of charge -0.8
C due to another small sphere of charge -0.8 ![]() C in air is 0.2 N. (a) What is the distance between the two spheres? (b) What is the force on the second sphere due to the first?
C in air is 0.2 N. (a) What is the distance between the two spheres? (b) What is the force on the second sphere due to the first?
Solution:
(a)
- Coulomb’s Law:

- Rearrange:

- Substitute:
 ,
,  ,
, 
- Calculate:





(b) By Newton’s Third Law, the force is equal in magnitude and opposite in direction.
Answer: (a) 12 cm, (b) 0.2 N (attractive)
Exercise 1.3
Question: Check that the ratio ![]() is dimensionless. Look up a Table of Physical Constants and determine the value of this ratio. What does the ratio signify?
is dimensionless. Look up a Table of Physical Constants and determine the value of this ratio. What does the ratio signify?
Solution:
- Dimensional Analysis:
![Rendered by QuickLaTeX.com [k] = [\text{N m}^2 \text{C}^{-2}] = [\text{ML}^3\text{T}^{-4}\text{I}^{-2}]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyNDciIGhlaWdodD0iMjEiIHZpZXdCb3g9IjAgMCAyNDcgMjEiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com [e] = [\text{IT}]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI2NyIgaGVpZ2h0PSIxOCIgdmlld0JveD0iMCAwIDY3IDE4Ij48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
![Rendered by QuickLaTeX.com [G] = [\text{N m}^2 \text{kg}^{-2}] = [\text{M}^{-1}\text{L}^3\text{T}^{-2}]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyNTAiIGhlaWdodD0iMjEiIHZpZXdCb3g9IjAgMCAyNTAgMjEiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com [m_e] = [m_p] = [\text{M}]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMzUiIGhlaWdodD0iMTkiIHZpZXdCb3g9IjAgMCAxMzUgMTkiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Therefore:
![Rendered by QuickLaTeX.com [\frac{k e^2}{G m_e m_p}] = \frac{[\text{ML}^3\text{T}^{-4}\text{I}^{-2}][\text{I}^2\text{T}^2]}{[\text{M}^{-1}\text{L}^3\text{T}^{-2}][\text{M}][\text{M}]} = [\text{M}^0\text{L}^0\text{T}^0\text{I}^0]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIzMTUiIGhlaWdodD0iMzIiIHZpZXdCb3g9IjAgMCAzMTUgMzIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+) → Dimensionless
→ Dimensionless
- Numerical Value:
 ,
,  ,
,  ,
,  ,
, 

- Significance: This ratio represents the strength of the electrostatic force to the gravitational force between an electron and a proton.
Answer: Dimensionless, value ![]() , ratio of electrostatic to gravitational force.
, ratio of electrostatic to gravitational force.
Exercise 1.4
(a) Electric charge is quantized means that any observable charge is an integral multiple of the elementary charge ![]() (
(![]() ).
).
(b) For macroscopic charges, the number of electrons transferred is so large that the discreteness (quantization) is not noticeable.
Exercise 1.5
Question: Explain how rubbing a glass rod with silk is consistent with the law of conservation of charge.
Solution: During rubbing, electrons are transferred from one body to another. The total charge before and after remains zero. The positive charge on one body is exactly equal to the negative charge on the other.
Exercise 1.6
Question: Four point charges ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are located at the corners of a square ABCD of side 10 cm. What is the force on a charge of 1
are located at the corners of a square ABCD of side 10 cm. What is the force on a charge of 1 ![]() C placed at the centre?
C placed at the centre?
Solution:
- The centre is equidistant from all corners.
- Forces due to
 and
and  are equal and opposite → cancel out.
are equal and opposite → cancel out. - Forces due to
 and
and  are equal and opposite → cancel out.
are equal and opposite → cancel out. - Net force = 0.
Answer: Zero
Exercise 1.7
(a) Electric field lines are continuous because the electric field is a continuous function in space. A break would imply no field, which isn’t true.
(b) Two field lines cannot cross because the electric field must have a unique direction at every point.
Exercise 1.8
Question: Two point charges ![]() and
and ![]() are located 20 cm apart in vacuum. (a) What is the electric field at the midpoint O? (b) If a negative test charge of magnitude
are located 20 cm apart in vacuum. (a) What is the electric field at the midpoint O? (b) If a negative test charge of magnitude ![]() is placed at O, what is the force experienced?
is placed at O, what is the force experienced?
Solution:
(a)
- At midpoint,
 from each charge.
from each charge. - Field due to
 :
:  (away from A, towards B)
(away from A, towards B) - Field due to
 :
:  (towards B)
(towards B) - Both fields are in the same direction (A→B), so
 (from A to B)
(from A to B)
(b)
- Force on test charge
 :
: 

- Since
 is negative, force is opposite to
is negative, force is opposite to  (from B to A)
(from B to A)
Answer: (a) ![]() (A→B), (b)
(A→B), (b) ![]() (B→A)
(B→A)
Exercise 1.9
Question: A system has two charges ![]() and
and ![]() at A: (0,0,-15 cm) and B: (0,0,+15 cm). What are the total charge and electric dipole moment?
at A: (0,0,-15 cm) and B: (0,0,+15 cm). What are the total charge and electric dipole moment?
Solution:
- Total charge:

- Dipole moment:


 from -q to +q = from A to B = (0,0,0.3) m
from -q to +q = from A to B = (0,0,0.3) m
- Direction: along +z axis
Answer: Total charge = 0, ![]()
Exercise 1.10
Question: An electric dipole with dipole moment ![]() is aligned at
is aligned at ![]() with a uniform electric field of magnitude
with a uniform electric field of magnitude ![]() . Calculate the torque.
. Calculate the torque.
Solution:
- Torque:

- Substitute:
 ,
,  ,
, 


Answer: ![]()
Exercise 1.11
Question: A polythene piece rubbed with wool has a negative charge of ![]() . (a) Estimate the number of electrons transferred. (b) Is there a transfer of mass?
. (a) Estimate the number of electrons transferred. (b) Is there a transfer of mass?
Solution:
(a)
 electrons
electrons- Electrons are transferred from wool to polythene.
(b) Yes, mass of electrons transferred:![]()
Answer: (a) ![]() electrons (wool to polythene), (b)
electrons (wool to polythene), (b) ![]()
Exercise 1.12
(a)
(b) If charge doubled and distance halved:![]()
Answer: (a) ![]() , (b)
, (b) ![]()
Exercise 1.13
Question: Figure 1.30 shows tracks of three charged particles in a uniform electrostatic field. Give the signs of the three charges. Which particle has the highest charge to mass ratio?
Solution:
- Positive charges deflect with the field, negative charges against it.
- The particle with the sharpest curvature has the highest charge-to-mass ratio (
 ).
).
(Without the figure, a general answer is provided)
Exercise 1.14
Question: Consider ![]() . (a) Flux through a square of side 10 cm parallel to the yz plane? (b) Flux if normal makes
. (a) Flux through a square of side 10 cm parallel to the yz plane? (b) Flux if normal makes ![]() with x-axis?
with x-axis?
Solution:
(a)
- Area

- Flux

(b)
Answer: (a) ![]() , (b)
, (b) ![]()
Exercise 1.15
Question: Net flux of the same field through a cube of side 20 cm with faces parallel to coordinate planes?
Solution:
- In a uniform field, the net flux through any closed surface is zero.
- Reason: Equal flux enters and exits the cube.
Answer: 0
Exercise 1.16
Question: Net outward flux through a black box is ![]() . (a) Net charge inside? (b) If flux were zero, could you conclude no charges inside?
. (a) Net charge inside? (b) If flux were zero, could you conclude no charges inside?
Solution:
(a)
- Gauss’s Law:


(b) No, there could be equal positive and negative charges inside (net charge zero).
Answer: (a) ![]() , (b) No
, (b) No
Exercise 1.17
Question: A point charge +10 ![]() C is 5 cm above the centre of a square of side 10 cm. Find flux through the square.
C is 5 cm above the centre of a square of side 10 cm. Find flux through the square.
Solution:
- Imagine the square as one face of a cube of side 10 cm with the charge at the centre.
- By symmetry, flux through each face is equal.
- Total flux through cube:

- Flux through one face:

Answer: ![]()
Exercise 1.18
Question: A point charge of 2.0 ![]() C at the centre of a cubic Gaussian surface 9.0 cm on edge. Net flux?
C at the centre of a cubic Gaussian surface 9.0 cm on edge. Net flux?
Solution:
- Gauss’s Law:


Answer: ![]()
Exercise 1.19
Question: A point charge causes a flux of ![]() through a spherical Gaussian surface of 10.0 cm radius. (a) Flux if radius doubled? (b) Value of charge?
through a spherical Gaussian surface of 10.0 cm radius. (a) Flux if radius doubled? (b) Value of charge?
Solution:
(a) Flux depends only on enclosed charge, not radius. So, flux remains ![]() .
.
(b)
Answer: (a) ![]() , (b)
, (b) ![]()
Exercise 1.20
Question: A conducting sphere of radius 10 cm has an unknown charge. Electric field 20 cm from centre is ![]() inward. Net charge on sphere?
inward. Net charge on sphere?
Solution:
- For a conducting sphere:



- Since field is inward, charge is negative.
Answer: ![]()
Exercise 1.21
Question: A uniformly charged conducting sphere of 2.4 m diameter has ![]() . (a) Charge on sphere? (b) Total flux leaving the surface?
. (a) Charge on sphere? (b) Total flux leaving the surface?
Solution:
(a)
- Radius

- Surface area

- Charge

(b)
Answer: (a) ![]() , (b)
, (b) ![]()
Exercise 1.22
Question: An infinite line charge produces ![]() at 2 cm. Calculate
at 2 cm. Calculate ![]() .
.
Solution:
- For infinite line charge:




Answer: ![]()
Exercise 1.23
Question: Two large parallel plates have surface charge densities ![]() and
and ![]() on inner faces. Find E in (a) outer region of first plate, (b) outer region of second plate, (c) between plates.
on inner faces. Find E in (a) outer region of first plate, (b) outer region of second plate, (c) between plates.
Solution:
- For two parallel plates with equal and opposite charges:
- Field outside the plates = 0
- Field between plates:

(a) ![]()
(b) ![]()
(c) ![]()
Answer: (a) 0, (b) 0, (c) ![]()
20 MCQs with Answers: Electric Charges and Fields
JEE‑oriented MCQs from NCERT Class 12 Physics Chapter 1 (Electric Charges and Fields).
- Quantisation check
A metal sphere carries charge . Which statement is most accurate?
. Which statement is most accurate?
A. may be any real number
may be any real number
B. must be an integer multiple of
must be an integer multiple of 
C. is an integer, but
is an integer, but  can appear continuous at macroscopic scale
can appear continuous at macroscopic scale
D. Quantisation holds only for insulators - Conservation in rubbing
When a glass rod is rubbed with silk, which process best describes what happens?
A. Protons flow from silk to glass; total charge increases
B. Electrons flow from glass to silk; total charge is conserved
C. Protons flow from glass to silk; total charge is conserved
D. Electrons flow from silk to glass; total charge decreases - Coulomb vector form
Charges at
at  and
and  at
at  . Force on
. Force on  due to
due to  is
is
A.
B.
C.
D. with
with  from 2 to 1
from 2 to 1 - Superposition
Which statement correctly expresses electrostatic superposition?
A. Forces add scalarly; direction is irrelevant
B. Each pairwise Coulomb force is unaffected by other charges; vector sum gives net force
C. A genuine three-body force appears for three charges
D. Net force depends only on total enclosed charge regardless of positions - Force ratio scale
For an electron–proton pair separated by , the ratio
, the ratio  equals
equals
A. (independent of
(independent of  )
)
B.
C.
D. Depends only on
- Field definition
Best operational definition of electric field at a point is
A. for any test charge
for any test charge 
B. to avoid disturbing sources
to avoid disturbing sources
C. by definition for all cases
by definition for all cases
D. equals force per unit mass
equals force per unit mass - Field lines
Which property of electrostatic field lines is correct?
A. They can intersect where fields superpose
B. They form closed loops in charge-free space
C. They never cross; local density indicates
D. They start on negative and end on positive charges - Flux element
Electric flux through a small oriented area with outward normal is
with outward normal is
A.
B.
C. for all orientations
for all orientations
D. for closed surfaces always
for closed surfaces always - Dipole far-field (axial)
At a distant axial point ( ) of a dipole with moment
) of a dipole with moment  , the field magnitude is
, the field magnitude is
A.
B.
C.
D.
- Dipole in uniform field
A rigid electric dipole in a uniform
in a uniform  experiences
experiences
A. Net force and zero torque
and zero torque
B. Zero force and zero torque for any orientation
C. Zero net force and torque
D. Net force toward higher if aligned
if aligned - Gauss’s law (global)
Total electric flux through any closed surface equals
A.
B.
C. Zero if the conductor is neutral
D. Depends on shape for the same enclosed charge - Infinite line charge
For an infinitely long straight wire with uniform linear density , the field at radial distance
, the field at radial distance  is
is
A.
B.
C.
D.
- Infinite plane sheet
A uniformly charged infinite plane sheet with surface density produces field magnitude
produces field magnitude
A. on each side, normal to the sheet
on each side, normal to the sheet
B. decreasing with distance
decreasing with distance
C. only near edges
only near edges
D. inside a conductor only
inside a conductor only - Spherical shell
For a thin uniformly charged spherical shell (total charge , radius
, radius  ), the field is
), the field is
A. for
for  and
and  for
for 
B. for
for  and
and  for
for 
C. Constant everywhere
D. Non-zero only at the centre - Continuous distribution integral
For a volume charge density , the field at
, the field at  is
is
A.
B.
C. (no constant)
(no constant)
D.
- Flux in non-uniform field
A cube of side occupies
occupies  . If
. If  , the net outward flux through the cube is
, the net outward flux through the cube is
A.
B.
C.
D.
- Atom-like model
A point charge at the centre of a sphere of radius
at the centre of a sphere of radius  is embedded in a uniform negative charge
is embedded in a uniform negative charge  spread throughout the sphere. For
spread throughout the sphere. For  , the radial field magnitude
, the radial field magnitude  is
is
A.
B.
C.
D.
- Dipole in gradient field
A permanent dipole aligned with placed in a non-uniform field experiences
placed in a non-uniform field experiences
A. Zero net force and nonzero torque
B. Force toward weaker field, torque zero
C. Force toward stronger field and torque when aligned
when aligned
D. Neither force nor torque - Sharing + distance change
Identical insulated spheres A and B initially carry each and are far apart. A is touched by an identical uncharged sphere C and B by an identical uncharged sphere D. After removing C and D, A and B are brought to half the original separation. The force between A and B becomes
each and are far apart. A is touched by an identical uncharged sphere C and B by an identical uncharged sphere D. After removing C and D, A and B are brought to half the original separation. The force between A and B becomes
A. Four times the original
B. Unchanged
C. One fourth of the original
D. Doubles - Flux by symmetry
A point charge is located a distance
is located a distance  above the centre of a square of side
above the centre of a square of side  . The electric flux through the square is
. The electric flux through the square is
A.
B.
C.
D. Depends on in a non-trivial way
in a non-trivial way
Answer Key with Explanations
- C. Charge is quantised:
 with integer
with integer  . For macroscopic
. For macroscopic  ,
,  appears continuous, but quantisation remains valid.
appears continuous, but quantisation remains valid. - B. Electrons transfer from glass to silk; glass loses electrons and becomes positive. Net charge of the isolated system is conserved.
- A. The correct vector form uses
 divided by its cube; it points along the line joining the charges with the correct inverse-square magnitude.
divided by its cube; it points along the line joining the charges with the correct inverse-square magnitude. - B. In electrostatics, each pairwise Coulomb force is independent of other charges; the net is the vector sum (no three-body term).
- A. Both forces vary as
 , hence the ratio
, hence the ratio  is independent of
is independent of  and extremely large.
and extremely large. - B. Using
 ensures the test charge does not disturb the source configuration.
ensures the test charge does not disturb the source configuration. - C. Field lines never cross (unique direction). Their density indicates field strength qualitatively.
- B. By definition,
 .
. - B. On the axis and for
 ,
,  .
. - C. In a uniform field, a dipole experiences zero net force but a torque
 .
. - B. Gauss’s law: total flux through a closed surface equals
 .
. - B. From Gauss’s law with cylindrical symmetry:
 , radial.
, radial. - A. For an infinite sheet,
 on each side, uniform and normal to the sheet.
on each side, uniform and normal to the sheet. - B. A thin charged shell behaves as a point charge externally; internally
 (for
(for  ).
). - B. Coulomb integral for a continuous volume charge:
 .
. - D. Only the
 -faces contribute:
-faces contribute: ![Rendered by QuickLaTeX.com \Phi=\big[\alpha x^2\big]_{0}^{a}a^2=\alpha a^4](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNTciIGhlaWdodD0iMjMiIHZpZXdCb3g9IjAgMCAxNTcgMjMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+) .
. - C. Enclosed negative charge at radius
 is
is  ; net enclosed
; net enclosed ![Rendered by QuickLaTeX.com =Ze[1-r^3/R^3]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMjUiIGhlaWdodD0iMjAiIHZpZXdCb3g9IjAgMCAxMjUgMjAiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+) gives
gives  .
. - C. In a non-uniform field, a dipole aligned with
 is pulled toward stronger field regions; torque is zero when aligned or anti-aligned.
is pulled toward stronger field regions; torque is zero when aligned or anti-aligned. - B. After sharing, A and B each have
 . Halving separation multiplies
. Halving separation multiplies  by
by  , but
, but  cancels it, leaving the force unchanged.
cancels it, leaving the force unchanged. - B. By symmetry (imagining a cube with the charge at its centre), each of the six faces receives flux
 .
.
CBSE PYQs: Electric Charges and Fields
Question 1: Charge Quantization (MCQ)
Source : CBSE Class 12, 2022-25, Paper Code 55(B), Question 1 (Section A), 1 Mark
Question: A charge of ![]() on a body represents (A) loss of
on a body represents (A) loss of ![]() electrons by the body. (B) gain of
electrons by the body. (B) gain of ![]() electrons by the body. (C) gain of
electrons by the body. (C) gain of ![]() electrons by the body. (D) loss of
electrons by the body. (D) loss of ![]() electrons by the body.
electrons by the body.
Solution:
- Identify the given charge and sign. The charge is
 . Since the charge is negative, the body has gained electrons.
. Since the charge is negative, the body has gained electrons. - Convert the charge magnitude to Coulombs:
![Rendered by QuickLaTeX.com \[Q = 1 \mu \text{C} = 1 \times 10^{-6} \text{ C}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNzkiIGhlaWdodD0iMjEiIHZpZXdCb3g9IjAgMCAxNzkgMjEiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Use the principle of quantisation of charge,
 , where
, where  is the number of electrons and
is the number of electrons and  is the magnitude of elementary charge (
is the magnitude of elementary charge ( ).
). ![Rendered by QuickLaTeX.com \[n = \frac{Q}{|e|}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI1NSIgaGVpZ2h0PSI0MiIgdmlld0JveD0iMCAwIDU1IDQyIj48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
- Substitute the values:
![Rendered by QuickLaTeX.com \[n = \frac{1 \times 10^{-6} \text{ C}}{1.6 \times 10^{-19} \text{ C}}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNDMiIGhlaWdodD0iMzkiIHZpZXdCb3g9IjAgMCAxNDMgMzkiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[n = \frac{1}{1.6} \times 10^{13} = 0.625 \times 10^{13}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyMzMiIGhlaWdodD0iMzYiIHZpZXdCb3g9IjAgMCAyMzMgMzYiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[n = 6.25 \times 10^{12} \text{ electrons}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxOTUiIGhlaWdodD0iMTciIHZpZXdCb3g9IjAgMCAxOTUgMTciPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Since the charge is negative, this represents a gain of electrons.
Final answer: (B) gain of ![]() electrons by the body.
electrons by the body.
Question 2: Electric Dipole Work
Source: CBSE Class 12, Paper Code 2155/4/3, 2022-25, Question 1 (Section A), 1 Mark
Question: An electric dipole of dipole moment ![]() is kept in a uniform electric field
is kept in a uniform electric field ![]() . The amount of work done to rotate it from the position of stable equilibrium to that of unstable equilibrium will be (A)
. The amount of work done to rotate it from the position of stable equilibrium to that of unstable equilibrium will be (A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D) zero
(D) zero
Solution:
- State the formula for the potential energy (
 ) of a dipole
) of a dipole  in a uniform electric field
in a uniform electric field  :
: ![Rendered by QuickLaTeX.com \[U = - \vec{p} \cdot \vec{E} = - \text{pE} \cos \theta\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxODUiIGhlaWdodD0iMjIiIHZpZXdCb3g9IjAgMCAxODUgMjIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Determine the initial position (stable equilibrium). This occurs when the dipole moment is aligned with the field (
 ).
). ![Rendered by QuickLaTeX.com \[U_i = - \text{pE} \cos(0^\circ) = - \text{pE}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxOTMiIGhlaWdodD0iMTkiIHZpZXdCb3g9IjAgMCAxOTMgMTkiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Determine the final position (unstable equilibrium). This occurs when the dipole moment is anti-parallel to the field (
 ).
). ![Rendered by QuickLaTeX.com \[U_f = - \text{pE} \cos(180^\circ) = - \text{pE} (-1) = + \text{pE}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIzMDkiIGhlaWdodD0iMjAiIHZpZXdCb3g9IjAgMCAzMDkgMjAiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Calculate the work done (
 ) to rotate the dipole:
) to rotate the dipole: ![Rendered by QuickLaTeX.com \[W = U_f - U_i\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMDMiIGhlaWdodD0iMTgiIHZpZXdCb3g9IjAgMCAxMDMgMTgiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[W = (\text{pE}) - (-\text{pE})\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNDkiIGhlaWdodD0iMTkiIHZpZXdCb3g9IjAgMCAxNDkgMTkiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[W = \text{pE} + \text{pE} = 2 \text{ pE}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNjgiIGhlaWdodD0iMTYiIHZpZXdCb3g9IjAgMCAxNjggMTYiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
Final answer: (A) ![]()
Question 3: Force Due to Infinite Line Charge
Source: CBSE Class 12, Paper Code 2155/4/3, 2022-25, Question 2 (Section A), 1 Mark
Question: An infinite long straight wire having a charge density ![]() is kept along
is kept along ![]() axis in
axis in ![]() plane. The Coulomb force on a point charge
plane. The Coulomb force on a point charge ![]() at a point
at a point ![]() will be (A) attractive and
will be (A) attractive and ![]() (B) repulsive and
(B) repulsive and ![]() (C) attractive and
(C) attractive and ![]() (D) repulsive and
(D) repulsive and ![]()
Solution:
- State the electric field (
 ) produced by an infinitely long straight wire with linear charge density
) produced by an infinitely long straight wire with linear charge density  at a perpendicular distance
at a perpendicular distance  (using Gauss’s Law):
(using Gauss’s Law): ![Rendered by QuickLaTeX.com \[E = \frac{\lambda}{2\pi\epsilon_0 x}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI4NCIgaGVpZ2h0PSIzOCIgdmlld0JveD0iMCAwIDg0IDM4Ij48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
- The force (
 ) exerted on a point charge
) exerted on a point charge  placed in this field is given by
placed in this field is given by  .
. ![Rendered by QuickLaTeX.com \[F = q \left( \frac{\lambda}{2\pi\epsilon_0 x} \right) = \frac{q\lambda}{2\pi\epsilon_0 x}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxOTQiIGhlaWdodD0iNDMiIHZpZXdCb3g9IjAgMCAxOTQgNDMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Determine the nature/direction of the force. The charge density
 is assumed positive (standard assumption unless otherwise specified, leading to an outward field), and the charge
is assumed positive (standard assumption unless otherwise specified, leading to an outward field), and the charge  is also usually assumed positive in the general case where direction is not provided, or simply relying on the magnitude calculation. Since the force formula is always proportional to
is also usually assumed positive in the general case where direction is not provided, or simply relying on the magnitude calculation. Since the force formula is always proportional to  , if
, if  and
and  have the same sign (both positive or both negative), the force will be repulsive (away from the wire, along the positive x-axis).
have the same sign (both positive or both negative), the force will be repulsive (away from the wire, along the positive x-axis). - Since the field formula matches Option (B), and repulsion is the case for charges of the same sign:
Final answer: (B) repulsive and ![]()
Question 4: Electric Field Calculation (Superposition Principle)
Source: CBSE Class 12, Paper Code 2255/5/2, 2022-25, Question 17 (b) OR (Section B), 2 Marks
Question: Three point charges, ![]() each, are kept at the vertices of an equilateral triangle of side
each, are kept at the vertices of an equilateral triangle of side ![]() . Find the net electric field at the centroid of triangle.
. Find the net electric field at the centroid of triangle.
Solution:
- Define the system: Three identical charges (
 ) placed at the vertices (A, B, C) of an equilateral triangle with side
) placed at the vertices (A, B, C) of an equilateral triangle with side  . We need the net electric field at the centroid (G).
. We need the net electric field at the centroid (G). ![Rendered by QuickLaTeX.com \[q_A = q_B = q_C = q = 1 \text{ pC}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxOTkiIGhlaWdodD0iMTYiIHZpZXdCb3g9IjAgMCAxOTkgMTYiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Determine the distance (
 ) from each vertex to the centroid (G). For an equilateral triangle,
) from each vertex to the centroid (G). For an equilateral triangle,  is the same for all vertices due to symmetry.
is the same for all vertices due to symmetry. ![Rendered by QuickLaTeX.com \[r = \frac{a}{\sqrt{3}}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI1OCIgaGVpZ2h0PSIzNiIgdmlld0JveD0iMCAwIDU4IDM2Ij48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
- Calculate the magnitude of the electric field (
 ) produced by each individual charge at the centroid G:
) produced by each individual charge at the centroid G: ![Rendered by QuickLaTeX.com \[E_A = E_B = E_C = E_0 = \frac{1}{4\pi\epsilon_0} \frac{q}{r^2}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyNDYiIGhlaWdodD0iMzkiIHZpZXdCb3g9IjAgMCAyNDYgMzkiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Determine the direction of the fields. Since all charges are positive, the field due to each charge points radially outwards, away from the charge, towards the opposite side of the triangle.
- Apply the superposition principle. At the centroid G, the three electric field vectors (
 ) have equal magnitude (
) have equal magnitude ( ) and are directed outwards, making
) and are directed outwards, making  angles with each other.
angles with each other. ![Rendered by QuickLaTeX.com \[|\vec{E}_A| = |\vec{E}_B| = |\vec{E}_C| = E_0\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxOTMiIGhlaWdodD0iMjMiIHZpZXdCb3g9IjAgMCAxOTMgMjMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- The vector sum of three equal magnitude vectors separated by
 is zero:
is zero: ![Rendered by QuickLaTeX.com \[\vec{E}_{\text{net}} = \vec{E}_A + \vec{E}_B + \vec{E}_C = 0\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyMDYiIGhlaWdodD0iMjAiIHZpZXdCb3g9IjAgMCAyMDYgMjAiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
Final answer: The net electric field at the centroid of the triangle is zero.
Question 5: Electric Field Calculation (Superposition Principle)
Source: CBSE Class 12, Paper Code 2255/5/1, 2022-25, Question 17 (a) (Section B), 2 Marks
Question: Four point charges of ![]() ,
, ![]() ,
, ![]() and
and ![]() are placed at the corners
are placed at the corners ![]() ,
, ![]() ,
, ![]() and
and ![]() respectively, of a square of side
respectively, of a square of side ![]() . Find the net force acting on a charge of
. Find the net force acting on a charge of ![]() placed at the centre of the square.
placed at the centre of the square.
Solution:
- Define the given charges and geometry:




 (Charge at the centre O) Side of square
(Charge at the centre O) Side of square  .
. - Determine the distance (
 ) from each corner to the centre (O). This distance is half the diagonal (
) from each corner to the centre (O). This distance is half the diagonal ( ).
). ![Rendered by QuickLaTeX.com \[d = a \sqrt{2}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI2NiIgaGVpZ2h0PSIxOCIgdmlld0JveD0iMCAwIDY2IDE4Ij48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
![Rendered by QuickLaTeX.com \[r = \frac{d}{2} = \frac{a \sqrt{2}}{2} = \frac{a}{\sqrt{2}}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNTYiIGhlaWdodD0iNDQiIHZpZXdCb3g9IjAgMCAxNTYgNDQiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[r = \frac{0.30 \text{ m}}{\sqrt{2}} \approx 0.212 \text{ m}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNzQiIGhlaWdodD0iNDAiIHZpZXdCb3g9IjAgMCAxNzQgNDAiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Apply the principle of superposition. The net force
 on
on  is the vector sum of forces from A, B, C, and D.
is the vector sum of forces from A, B, C, and D. ![Rendered by QuickLaTeX.com \[\vec{F}</em>{\text{net}} = \vec{F}<em>{OA} + \vec{F}</em>{OB} + \vec{F}<em>{OC} + \vec{F}</em>{OD}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI2NTQiIGhlaWdodD0iMjMiIHZpZXdCb3g9IjAgMCA2NTQgMjMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Compare forces exerted by opposite pairs (A and C, B and D):
- Force due to A (
 ) and C (
) and C ( ): Since
): Since  and the distance
and the distance  is the same, the magnitudes of force
is the same, the magnitudes of force  and
and  are equal. Since both
are equal. Since both  and
and  are positive, they both repel the central positive charge
are positive, they both repel the central positive charge  .
.  points away from A (towards C), and
points away from A (towards C), and  points away from C (towards A). Since they are equal in magnitude and opposite in direction:
points away from C (towards A). Since they are equal in magnitude and opposite in direction: ![Rendered by QuickLaTeX.com \[\vec{F}<em>{AC} = \vec{F}</em>{OA} + \vec{F}_{OC} = 0\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIzNDUiIGhlaWdodD0iMjMiIHZpZXdCb3g9IjAgMCAzNDUgMjMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Force due to B (
 ) and D (
) and D ( ): Since
): Since  and the distance
and the distance  is the same, the magnitudes of force
is the same, the magnitudes of force  and
and  are equal. Since
are equal. Since  and
and  are negative, they both attract the central positive charge
are negative, they both attract the central positive charge  .
.  points towards B, and
points towards B, and  points towards D. Since they are equal in magnitude and opposite in direction:
points towards D. Since they are equal in magnitude and opposite in direction: ![Rendered by QuickLaTeX.com \[\vec{F}<em>{BD} = \vec{F}</em>{OB} + \vec{F}_{OD} = 0\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIzNTAiIGhlaWdodD0iMjMiIHZpZXdCb3g9IjAgMCAzNTAgMjMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Force due to A (
- Calculate the net force:
![Rendered by QuickLaTeX.com \[\vec{F}<em>{\text{net}} = \vec{F}</em>{AC} + \vec{F}_{BD} = 0 + 0 = 0\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI0MDYiIGhlaWdodD0iMjMiIHZpZXdCb3g9IjAgMCA0MDYgMjMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
Final answer: The net force acting on the charge placed at the centre of the square is zero.
(Note: Questions 18 in 55/5/2 and 17(a) in 55/5/2 are identical to Question 15, confirming the zero net force due to charge and geometric symmetry.)
Question 6: Electric Field/Force (Work Done)
Source: CBSE Class 12, Paper Code 55/2/2, 2022-25, Question 16 (Assertion/Reason) (Section A), 1 Mark
Question: Assertion (A) : Work done in moving a charge around a closed path, in an electric field is always zero. Reason (R) : Electrostatic force is a conservative force.
Solution:
- Analyze Assertion (A): Work done
 in moving a charge
in moving a charge  between two points A and B is defined by the negative change in potential energy,
between two points A and B is defined by the negative change in potential energy,  . For a closed path, the final point is the initial point, so
. For a closed path, the final point is the initial point, so  . Hence,
. Hence,  . Assertion (A) is true.
. Assertion (A) is true. - Analyze Reason (R): A conservative force is one where the work done depends only on the initial and final positions, and is zero around a closed path. Electrostatic force is, by definition, a conservative force. Reason (R) is true.
- Evaluate the relationship: The assertion (work done is zero in a closed path) is a direct consequence of the electrostatic force being conservative.
Final answer: Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
Question 7: Gauss’s Law (Electric Flux through a Cube Face)
Source: CBSE Class 12, Paper Code 55/5/2, 2022-25, Question 1 (Section A), 1 Mark
Question: A charge ![]() is placed at the centre of a cube. The electric flux through one if its face is (A)
is placed at the centre of a cube. The electric flux through one if its face is (A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
Solution:
- State Gauss’s Law: The total electric flux (
 ) passing through a closed surface (Gaussian surface) is equal to
) passing through a closed surface (Gaussian surface) is equal to  times the net charge (
times the net charge ( ) enclosed within that surface.
) enclosed within that surface. ![Rendered by QuickLaTeX.com \[\Phi_{\text{total}} = \frac{Q_{\text{enclosed}}}{\epsilon_0}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMzIiIGhlaWdodD0iMzkiIHZpZXdCb3g9IjAgMCAxMzIgMzkiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- For a charge
 placed exactly at the centre of a cube, the cube acts as the closed Gaussian surface. Thus, the total flux through the entire cube is:
placed exactly at the centre of a cube, the cube acts as the closed Gaussian surface. Thus, the total flux through the entire cube is: ![Rendered by QuickLaTeX.com \[\Phi_{\text{cube}} = \frac{Q}{\epsilon_0}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI4MiIgaGVpZ2h0PSIzOSIgdmlld0JveD0iMCAwIDgyIDM5Ij48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
- Due to the perfect symmetry of the cube, the total flux must be equally distributed across its six identical faces.
![Rendered by QuickLaTeX.com \[\Phi_{\text{one face}} = \frac{\Phi_{\text{cube}}}{6}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMzAiIGhlaWdodD0iMzciIHZpZXdCb3g9IjAgMCAxMzAgMzciPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Substitute the total flux:
![Rendered by QuickLaTeX.com \[\Phi_{\text{one face}} = \frac{Q}{6\epsilon_0}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMTIiIGhlaWdodD0iMzkiIHZpZXdCb3g9IjAgMCAxMTIgMzkiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
Final answer: (B) ![]()
Question 8: Gauss’s Law Application (Infinite Wire)
Source: CBSE Class 12, Paper Code 55/2/1, 2022-25, Question 31 (a)(i) OR (Section D), 5 Marks
Question: Use Gauss’ law to obtain an expression for the electric field due to an infinitely long thin straight wire with uniform linear charge density ![]() .
.
Solution:
- Choose Gaussian Surface: Consider an infinitely long, thin straight wire having a uniform linear charge density
 . By symmetry, the electric field
. By symmetry, the electric field  must be radial (perpendicular to the wire) and constant in magnitude at any fixed distance
must be radial (perpendicular to the wire) and constant in magnitude at any fixed distance  from the wire. We choose a co-axial cylindrical Gaussian surface of radius
from the wire. We choose a co-axial cylindrical Gaussian surface of radius  and arbitrary length
and arbitrary length  .
. - Apply Gauss’s Law: Gauss’s Law states:
![Rendered by QuickLaTeX.com \[\Phi = \oint \vec{E} \cdot d\vec{S} = \frac{Q_{\text{enclosed}}}{\epsilon_0}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxOTYiIGhlaWdodD0iNDAiIHZpZXdCb3g9IjAgMCAxOTYgNDAiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Calculate Total Flux (
 ): The cylindrical surface has three parts: the curved surface (
): The cylindrical surface has three parts: the curved surface ( ) and the two flat circular end caps (
) and the two flat circular end caps ( and
and  ).
). ![Rendered by QuickLaTeX.com \[\Phi = \oint_{S_1} \vec{E} \cdot d\vec{S} + \oint_{S_2} \vec{E} \cdot d\vec{S} + \oint_{S_3} \vec{E} \cdot d\vec{S}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIzMTIiIGhlaWdodD0iNDIiIHZpZXdCb3g9IjAgMCAzMTIgNDIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- For the end caps (
 ):
):  is perpendicular to
is perpendicular to  (parallel to the surface), so
(parallel to the surface), so  .
.  . The flux through the end caps is zero.
. The flux through the end caps is zero. - For the curved surface (
 ):
):  is parallel to
is parallel to  (radially outwards), so
(radially outwards), so  .
.  . Since
. Since  is constant on the curved surface:
is constant on the curved surface: ![Rendered by QuickLaTeX.com \[\Phi = E \oint_{S_1} dS = E (2\pi r l)\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxODciIGhlaWdodD0iNDIiIHZpZXdCb3g9IjAgMCAxODcgNDIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- For the end caps (
- Calculate Enclosed Charge (
 ): The charge enclosed within the length
): The charge enclosed within the length  of the wire is:
of the wire is: ![Rendered by QuickLaTeX.com \[Q_{\text{enclosed}} = \lambda l\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMDMiIGhlaWdodD0iMTYiIHZpZXdCb3g9IjAgMCAxMDMgMTYiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Equate Flux and Charge: Equating the expressions from steps 2, 3, and 4:
![Rendered by QuickLaTeX.com \[E (2\pi r l) = \frac{\lambda l}{\epsilon_0}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMDMiIGhlaWdodD0iMzgiIHZpZXdCb3g9IjAgMCAxMDMgMzgiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Solve for E: Rearranging the equation to find the electric field
 :
: ![Rendered by QuickLaTeX.com \[E = \frac{\lambda l}{2\pi \epsilon_0 r l}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI4OCIgaGVpZ2h0PSIzOCIgdmlld0JveD0iMCAwIDg4IDM4Ij48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
The electric field![Rendered by QuickLaTeX.com \[E = \frac{\lambda}{2\pi \epsilon_0 r}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI4MiIgaGVpZ2h0PSIzOCIgdmlld0JveD0iMCAwIDgyIDM4Ij48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
 is directed radially outward (if
is directed radially outward (if  is positive).
is positive).
Final answer: The expression for the electric field is ![]() .
.
Question 9: Electric Force and Kinematics (Circular Motion)
Source: CBSE Class 12, Paper Code 55/2/1, 2022-25, Question 31 (a)(ii) (Section D), 5 Marks
Question: An infinitely long positively charged straight wire has a linear charge density ![]() . An electron is revolving in a circle with a constant speed
. An electron is revolving in a circle with a constant speed ![]() such that the wire passes through the centre, and is perpendicular to the plane, of the circle. Find the kinetic energy of the electron in terms of magnitudes of its charge and linear charge density
such that the wire passes through the centre, and is perpendicular to the plane, of the circle. Find the kinetic energy of the electron in terms of magnitudes of its charge and linear charge density ![]() on the wire.
on the wire.
Solution:
- Identify the forces: The electron (charge
 ) revolves around the wire at a distance
) revolves around the wire at a distance  . The centripetal force required for circular motion is provided by the electrostatic force (
. The centripetal force required for circular motion is provided by the electrostatic force ( ) exerted by the charged wire on the electron. Since the wire is positively charged (
) exerted by the charged wire on the electron. Since the wire is positively charged ( is positive) and the electron is negative (
is positive) and the electron is negative ( ), the force is attractive and directed radially towards the wire (i.e., acting as the centripetal force).
), the force is attractive and directed radially towards the wire (i.e., acting as the centripetal force). - State the Electric Field (E): From Gauss’s law (Q8), the magnitude of the electric field at distance
 from the wire is:
from the wire is: ![Rendered by QuickLaTeX.com \[E = \frac{\lambda}{2\pi \epsilon_0 r}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI4MiIgaGVpZ2h0PSIzOCIgdmlld0JveD0iMCAwIDgyIDM4Ij48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
- Equate Forces: The electrostatic force
 must equal the centripetal force
must equal the centripetal force  :
: ![Rendered by QuickLaTeX.com \[F_e = F_c\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI1OSIgaGVpZ2h0PSIxNCIgdmlld0JveD0iMCAwIDU5IDE0Ij48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
![Rendered by QuickLaTeX.com \[e E = \frac{m_e v^2}{r}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI4OCIgaGVpZ2h0PSIzOSIgdmlld0JveD0iMCAwIDg4IDM5Ij48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
- Substitute E and Solve for Kinetic Energy (K): Kinetic Energy is
 . We substitute the expression for
. We substitute the expression for  into the force equation:
into the force equation: ![Rendered by QuickLaTeX.com \[e \left( \frac{\lambda}{2\pi \epsilon_0 r} \right) = \frac{m_e v^2}{r}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNTAiIGhlaWdodD0iNDQiIHZpZXdCb3g9IjAgMCAxNTAgNDQiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Rearrange the equation to isolate
 :
: ![Rendered by QuickLaTeX.com \[\frac{e \lambda}{2\pi \epsilon_0 r} = \frac{m_e v^2}{r}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMTAiIGhlaWdodD0iNDIiIHZpZXdCb3g9IjAgMCAxMTAgNDIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[m_e v^2 = \frac{e \lambda}{2\pi \epsilon_0}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMDAiIGhlaWdodD0iMzgiIHZpZXdCb3g9IjAgMCAxMDAgMzgiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Find the kinetic energy
 :
: ![Rendered by QuickLaTeX.com \[K = \frac{1}{2} m_e v^2 = \frac{1}{2} \left( \frac{e \lambda}{2\pi \epsilon_0} \right)\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxOTMiIGhlaWdodD0iNDMiIHZpZXdCb3g9IjAgMCAxOTMgNDMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[K = \frac{e \lambda}{4\pi \epsilon_0}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI3NyIgaGVpZ2h0PSIzOCIgdmlld0JveD0iMCAwIDc3IDM4Ij48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
Final answer: The kinetic energy of the electron is ![]() .
.
Question 10: Work Done in Non-Uniform Electric Field
Source: CBSE Class 12, Paper Code 2155/4/1, 2022-25, Question 23 (Section C), 3 Marks
Question: The electric field in a region is given by
![]()
Solution: The work done ![]() in moving a charge
in moving a charge ![]() along a path
along a path ![]() in an electric field
in an electric field ![]() is given by:
is given by:
![]()
![]()
(i) Work done from  to
to  :
:
- Set up the integral for the work done
 :
: ![Rendered by QuickLaTeX.com \[W = - (1 \text{ C}) \int_{x=5}^{x=10} (10x + 4) dx\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyNDMiIGhlaWdodD0iNDQiIHZpZXdCb3g9IjAgMCAyNDMgNDQiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Integrate the expression:
![Rendered by QuickLaTeX.com \[W = - \left[ \frac{10x^2}{2} + 4x \right]<em>{5}^{10} = - \left[ 5x^2 + 4x \right]</em>{5}^{10}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI0NzkiIGhlaWdodD0iNDQiIHZpZXdCb3g9IjAgMCA0NzkgNDQiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Substitute the limits:
![Rendered by QuickLaTeX.com \[W = - \left[ (5(10)^2 + 4(10)) - (5(5)^2 + 4(5)) \right]\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIzMjMiIGhlaWdodD0iMjMiIHZpZXdCb3g9IjAgMCAzMjMgMjMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[W = - \left[ (500 + 40) - (125 + 20) \right]\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyNDkiIGhlaWdodD0iMTkiIHZpZXdCb3g9IjAgMCAyNDkgMTkiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[W = - \left[ 540 - 145 \right]\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNDIiIGhlaWdodD0iMTgiIHZpZXdCb3g9IjAgMCAxNDIgMTgiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[W = - 395 \text{ J}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI5OCIgaGVpZ2h0PSIxMyIgdmlld0JveD0iMCAwIDk4IDEzIj48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
Final answer (i): ![]()
(ii) Work done from  to
to  :
:
- Analyze the path: The initial position is
 and the final position is
and the final position is  . Along this path, the displacement is purely vertical (
. Along this path, the displacement is purely vertical ( ), meaning
), meaning  .
. - Calculate the dot product
 :
:
Since![Rendered by QuickLaTeX.com \[\vec{E} \cdot d\vec{l} = (10x + 4) dx\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNTciIGhlaWdodD0iMjMiIHZpZXdCb3g9IjAgMCAxNTcgMjMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
 :
: ![Rendered by QuickLaTeX.com \[\vec{E} \cdot d\vec{l} = 0\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI3NCIgaGVpZ2h0PSIxOCIgdmlld0JveD0iMCAwIDc0IDE4Ij48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
- Calculate the work done:
![Rendered by QuickLaTeX.com \[W = - q \int \vec{E} \cdot d\vec{l} = 0 \text{ J}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNzgiIGhlaWdodD0iNDAiIHZpZXdCb3g9IjAgMCAxNzggNDAiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
Final answer (ii): ![]()
Question 11: Electric Flux and Net Enclosed Charge in a Non-Uniform Field
Source: CBSE Class 12, Paper Code 2155/4/1, 2022-25, Question 32 (b)(ii) (Section E), 5 Marks
Question: Electric field ![]() in a region is given by
in a region is given by
![]()
Figure missing: (The figure describes a cube placed in the first octant, with one corner at the origin (0, 0, 0) and edges aligned along the x, y, and z axes. Side length ![]() .)
.)
Solution: Given ![]() .
. ![]() . The electric field is uniform only in the sense that it only varies with
. The electric field is uniform only in the sense that it only varies with ![]() .
.
(1) Calculate the electric flux through the cube ( )
)
- Analyze flux components: Since the electric field
 is along the
is along the  -axis (
-axis ( direction), flux passes only through the two faces perpendicular to the
direction), flux passes only through the two faces perpendicular to the  -axis (the ‘Left’ face at
-axis (the ‘Left’ face at  and the ‘Right’ face at
and the ‘Right’ face at  ). The flux through the four remaining faces (parallel to the
). The flux through the four remaining faces (parallel to the  -axis) is zero because
-axis) is zero because  .
. - Calculate Flux through Left Face (
 ): The area vector
): The area vector  points along
points along  .
. ![Rendered by QuickLaTeX.com \[E</em>{\text{Left}} = (5(0)^2 + 2) \hat{i} = 2 \hat{i} \text{ N/C}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIzMTciIGhlaWdodD0iMjIiIHZpZXdCb3g9IjAgMCAzMTcgMjIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[A = a^2 = (0.1)^2 = 0.01 \text{ m}^2\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyMDUiIGhlaWdodD0iMjIiIHZpZXdCb3g9IjAgMCAyMDUgMjIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[\Phi_{\text{Left}} = \vec{E}<em>{\text{Left}} \cdot \vec{A}</em>{\text{Left}} = (2 \hat{i}) \cdot (-(0.01) \hat{i})\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI0NTkiIGhlaWdodD0iMjMiIHZpZXdCb3g9IjAgMCA0NTkgMjMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[\Phi_{\text{Left}} = -0.02 \text{ N m}^2/\text{C}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNzUiIGhlaWdodD0iMjIiIHZpZXdCb3g9IjAgMCAxNzUgMjIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Calculate Flux through Right Face (
 ): The area vector
): The area vector  points along
points along  .
. ![Rendered by QuickLaTeX.com \[E</em>{\text{Right}} = (5(0.1)^2 + 2) \hat{i} \text{ N/C}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIzMDQiIGhlaWdodD0iMjIiIHZpZXdCb3g9IjAgMCAzMDQgMjIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[E_{\text{Right}} = (5(0.01) + 2) \hat{i} = 2.05 \hat{i} \text{ N/C}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyNzciIGhlaWdodD0iMjIiIHZpZXdCb3g9IjAgMCAyNzcgMjIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[\Phi_{\text{Right}} = \vec{E}<em>{\text{Right}} \cdot \vec{A}</em>{\text{Right}} = (2.05 \hat{i}) \cdot ((0.01) \hat{i})\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI1MDEiIGhlaWdodD0iMjMiIHZpZXdCb3g9IjAgMCA1MDEgMjMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[\Phi_{\text{Right}} = +0.0205 \text{ N m}^2/\text{C}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyMDMiIGhlaWdodD0iMjMiIHZpZXdCb3g9IjAgMCAyMDMgMjMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Calculate Net Flux (
 ):
): ![Rendered by QuickLaTeX.com \[\Phi_{\text{net}} = \Phi_{\text{Left}} + \Phi_{\text{Right}}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNjIiIGhlaWdodD0iMTgiIHZpZXdCb3g9IjAgMCAxNjIgMTgiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[\Phi_{\text{net}} = -0.02 \text{ N m}^2/\text{C} + 0.0205 \text{ N m}^2/\text{C}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIzMTEiIGhlaWdodD0iMjIiIHZpZXdCb3g9IjAgMCAzMTEgMjIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[\Phi_{\text{net}} = 0.0005 \text{ N m}^2/\text{C}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNzUiIGhlaWdodD0iMjIiIHZpZXdCb3g9IjAgMCAxNzUgMjIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
Final answer (1): The electric flux through the cube is ![]() .
.
(2) Calculate the net charge enclosed by the cube ( )
)
- Use Gauss’s Law to relate net flux and enclosed charge:
![Rendered by QuickLaTeX.com \[\Phi_{\text{net}} = \frac{Q_{\text{enclosed}}}{\epsilon_0}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMjQiIGhlaWdodD0iMzkiIHZpZXdCb3g9IjAgMCAxMjQgMzkiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[Q_{\text{enclosed}} = \Phi_{\text{net}} \epsilon_0\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMzUiIGhlaWdodD0iMTYiIHZpZXdCb3g9IjAgMCAxMzUgMTYiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Substitute the values (
 ):
): ![Rendered by QuickLaTeX.com \[Q_{\text{enclosed}} = (0.0005 \text{ N m}^2/\text{C}) \times (8.854 \times 10^{-12} \text{ C}^2 \text{ N}^{-1} \text{ m}^{-2})\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI0NjMiIGhlaWdodD0iMjIiIHZpZXdCb3g9IjAgMCA0NjMgMjIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[Q_{\text{enclosed}} = 5 \times 10^{-4} \times 8.854 \times 10^{-12} \text{ C}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyOTkiIGhlaWdodD0iMjEiIHZpZXdCb3g9IjAgMCAyOTkgMjEiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[Q_{\text{enclosed}} = 44.27 \times 10^{-16} \text{ C}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyMTEiIGhlaWdodD0iMjEiIHZpZXdCb3g9IjAgMCAyMTEgMjEiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[Q_{\text{enclosed}} \approx 4.427 \times 10^{-15} \text{ C}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyMTEiIGhlaWdodD0iMjEiIHZpZXdCb3g9IjAgMCAyMTEgMjEiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
Final answer (2): The net charge enclosed by the cube is approximately ![]() .
.
Question 12: Gauss’s Law (Flux through Concentric Shells)
Source: CBSE Class 12, Paper Code 55/2/1, 2022-25, Question 32 (b)(iii) OR (Section E), 5 Marks
Question: A small spherical shell ![]() has point charges
has point charges ![]() ,
, ![]() and
and ![]() inside it. This shell is enclosed by another big spherical shell
inside it. This shell is enclosed by another big spherical shell ![]() . A point charge
. A point charge ![]() is placed in between the two surfaces
is placed in between the two surfaces ![]() and
and ![]() . If the electric flux through the surface
. If the electric flux through the surface ![]() is four times the flux through surface
is four times the flux through surface ![]() , find charge
, find charge ![]() .
.
Solution:
- Calculate charge enclosed by
 (
( ):
): ![Rendered by QuickLaTeX.com \[Q_{\text{encl}, 1} = q_1 + q_2 + q_3\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNjMiIGhlaWdodD0iMTgiIHZpZXdCb3g9IjAgMCAxNjMgMTgiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[Q_{\text{encl}, 1} = (-3 \mu\text{C}) + (-2 \mu\text{C}) + (9 \mu\text{C})\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyODEiIGhlaWdodD0iMjAiIHZpZXdCb3g9IjAgMCAyODEgMjAiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[Q_{\text{encl}, 1} = 4 \mu\text{C}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMDUiIGhlaWdodD0iMTgiIHZpZXdCb3g9IjAgMCAxMDUgMTgiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Calculate flux through
 (
( ): Using Gauss’s Law:
): Using Gauss’s Law: ![Rendered by QuickLaTeX.com \[\Phi_1 = \frac{Q_{\text{encl}, 1}}{\epsilon_0} = \frac{4 \mu\text{C}}{\epsilon_0}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNTYiIGhlaWdodD0iNDAiIHZpZXdCb3g9IjAgMCAxNTYgNDAiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Calculate charge enclosed by
 (
( ):
):  encloses
encloses  , and the charge
, and the charge  placed between
placed between  and
and  .
. ![Rendered by QuickLaTeX.com \[Q{\text{encl}, 2} = q_1 + q_2 + q_3 + Q\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyMTEiIGhlaWdodD0iMTYiIHZpZXdCb3g9IjAgMCAyMTEgMTYiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[Q</em>{\text{encl}, 2} = 4 \mu\text{C} + Q\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyMzMiIGhlaWdodD0iMTkiIHZpZXdCb3g9IjAgMCAyMzMgMTkiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Calculate flux through
 (
( ):
): ![Rendered by QuickLaTeX.com \[\Phi_2 = \frac{Q_{\text{encl}, 2}}{\epsilon_0} = \frac{4 \mu\text{C} + Q}{\epsilon_0}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxOTIiIGhlaWdodD0iNDAiIHZpZXdCb3g9IjAgMCAxOTIgNDAiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Use the given condition: The electric flux through
 is four times the flux through
is four times the flux through  :
: ![Rendered by QuickLaTeX.com \[\Phi_2 = 4 \Phi_1\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI3MiIgaGVpZ2h0PSIxNCIgdmlld0JveD0iMCAwIDcyIDE0Ij48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
- Solve for Q:
![Rendered by QuickLaTeX.com \[\frac{4 \mu\text{C} + Q}{\epsilon_0} = 4 \left( \frac{4 \mu\text{C}}{\epsilon_0} \right)\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNjUiIGhlaWdodD0iNDMiIHZpZXdCb3g9IjAgMCAxNjUgNDMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[4 \mu\text{C} + Q = 16 \mu\text{C}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMzMiIGhlaWdodD0iMTYiIHZpZXdCb3g9IjAgMCAxMzMgMTYiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[Q = 16 \mu\text{C} - 4 \mu\text{C}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMzMiIGhlaWdodD0iMTYiIHZpZXdCb3g9IjAgMCAxMzMgMTYiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[Q = 12 \mu\text{C}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI3OSIgaGVpZ2h0PSIxNiIgdmlld0JveD0iMCAwIDc5IDE2Ij48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
Final answer: The charge ![]() is
is ![]() .
.
Question 13: Electric Field due to Point Charges (Conceptual/MCQ)
Source: CBSE Class 12, Paper Code 2255/5/2, 2022-25, Question 15 (Assertion/Reason) (Section A), 1 Mark
Question: Assertion (A) : Equal amount of positive and negative charges are distributed uniformly on two halves of a thin circular ring as shown in figure. The resultant electric field at the centre O of the ring is along OC. Reason (R) : It is so because the net potential at O is not zero.
Figure missing: (The figure shows a circular ring centered at O. The upper semi-circle (say A-B-D, moving clockwise) is labeled with positive charges, and the lower semi-circle (say A-C-D) is labeled with negative charges. C is at the bottom, and the line segment OC points downwards).
Solution:
- Analyze Assertion (A) (Electric Field): Due to symmetry, the horizontal components of the electric field (
 ) created by the charges cancel out. Both the positive charge on the top half and the negative charge on the bottom half create a net electric field component pointing downwards (along the direction OC).
) created by the charges cancel out. Both the positive charge on the top half and the negative charge on the bottom half create a net electric field component pointing downwards (along the direction OC).
- Positive charges repel a test charge down.
- Negative charges attract a test charge down.
- Therefore, the resultant electric field at the centre O is along OC (downwards). Assertion (A) is true.
- Analyze Reason (R) (Electric Potential): Electric potential (
 ) is a scalar quantity. Potential at O is the sum of potentials due to positive charges (
) is a scalar quantity. Potential at O is the sum of potentials due to positive charges ( ) and negative charges (
) and negative charges ( ). Since the positive charge magnitude (
). Since the positive charge magnitude ( ) equals the negative charge magnitude (
) equals the negative charge magnitude ( ), and all charges are equidistant (
), and all charges are equidistant ( ) from the centre O:
) from the centre O:
The net potential at O is zero. Reason (R) states the net potential is not zero. Reason (R) is false.![Rendered by QuickLaTeX.com \[V_{\text{net}} = V_{\text{pos}} + V_{\text{neg}} = \frac{k(+Q)}{R} + \frac{k(-Q)}{R} = 0\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIzMjgiIGhlaWdodD0iMzgiIHZpZXdCb3g9IjAgMCAzMjggMzgiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Conclusion: Assertion (A) is true, but Reason (R) is false.
Final answer: (C) Assertion (A) is true, but Reason (R) is false.
Question 14: Force/Distance Relation (Coulomb’s Law Graph)
Source: CBSE Class 12, Paper Code 2155/4/2, 2022-25, Question 2 (Section A), 1 Mark
Question: The Coulomb force (F) versus ![]() graphs for two pairs of point charges
graphs for two pairs of point charges ![]() and
and ![]() are shown in figure. The charge
are shown in figure. The charge ![]() is positive and has least magnitude. Then (A)
is positive and has least magnitude. Then (A) ![]() (B)
(B) ![]() (C)
(C) ![]() (Repeat of B, likely error in source options) (D)
(Repeat of B, likely error in source options) (D) ![]()
Figure missing: (The figure shows a graph of Force F (y-axis) vs ![]() (x-axis). A straight line labeled
(x-axis). A straight line labeled ![]() has a positive slope, and a straight line labeled
has a positive slope, and a straight line labeled ![]() has a negative slope.)
has a negative slope.)
Solution:
- Relate F to
 : Coulomb’s Law magnitude is
: Coulomb’s Law magnitude is  . This gives a linear relationship between
. This gives a linear relationship between  and
and  .
.
The slope of the![Rendered by QuickLaTeX.com \[F = \text{Constant} \times \frac{1}{r^2}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNDkiIGhlaWdodD0iMzYiIHZpZXdCb3g9IjAgMCAxNDkgMzYiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
 vs
vs  graph is proportional to the magnitude of the product of the charges:
graph is proportional to the magnitude of the product of the charges:  .
. - Analyze the Signs (Attraction/Repulsion):
- The line for
 has a positive slope (F increases as
has a positive slope (F increases as  increases, and F is plotted as positive/magnitude). Since
increases, and F is plotted as positive/magnitude). Since  is positive, for the force to be plotted in the positive F region, we assume the graph shows the magnitude of the force. We cannot definitively determine the sign relationship from the visual information provided without specific labeling conventions, but for magnitude comparison, we rely on the slope magnitude.
is positive, for the force to be plotted in the positive F region, we assume the graph shows the magnitude of the force. We cannot definitively determine the sign relationship from the visual information provided without specific labeling conventions, but for magnitude comparison, we rely on the slope magnitude. - Reinterpreting typical convention: If
 represents repulsive force (positive
represents repulsive force (positive  ) and attractive force (negative
) and attractive force (negative  ). Let’s assume the question implies comparison of magnitudes of slopes
). Let’s assume the question implies comparison of magnitudes of slopes  .
.
- The line for
- Analyze Slope Magnitudes: Let
 be the slope for
be the slope for  and
and  be the slope for
be the slope for  . Based on the visual description (Line
. Based on the visual description (Line  appears to have a steeper magnitude of slope than
appears to have a steeper magnitude of slope than  if the graph lines are plotted on the same axes, implying
if the graph lines are plotted on the same axes, implying  ). Assuming the visual evidence (if present) confirms
). Assuming the visual evidence (if present) confirms  :
: ![Rendered by QuickLaTeX.com \[|q_2 q_3| > |q_1 q_2|\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMDIiIGhlaWdodD0iMTkiIHZpZXdCb3g9IjAgMCAxMDIgMTkiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Use Given Information: We are given that
 is positive and has the least magnitude:
is positive and has the least magnitude: ![Rendered by QuickLaTeX.com \[|q_2| < |q_1| \text{ and } |q_2| < |q_3|\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxODYiIGhlaWdodD0iMTkiIHZpZXdCb3g9IjAgMCAxODYgMTkiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Compare
 and
and  : If
: If  , dividing by
, dividing by  (which is the smallest charge magnitude) yields:
(which is the smallest charge magnitude) yields: ![Rendered by QuickLaTeX.com \[|q_3| > |q_1|\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI3MCIgaGVpZ2h0PSIxOSIgdmlld0JveD0iMCAwIDcwIDE5Ij48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
- Order the charges by magnitude: Combining the constraints:
Therefore,![Rendered by QuickLaTeX.com \[|q_3| > |q_1| > |q_2|\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMjAiIGhlaWdodD0iMTkiIHZpZXdCb3g9IjAgMCAxMjAgMTkiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
 has the greatest magnitude, followed by
has the greatest magnitude, followed by  , and then
, and then  .
.
Final answer: (D) ![]() (assuming
(assuming ![]() represents the magnitude
represents the magnitude ![]() , consistent with the context that
, consistent with the context that ![]() has the least magnitude).
has the least magnitude).
Question 15: Potential Energy of a Dipole (Work Done)
Source: CBSE Class 12, Paper Code 2155/5/2, 2022-25, Question 32 (b)(iii) (in Hindi, refers to Dipole Moment ![]() and
and ![]() )
)
Question (Reconstructed from English source 59, Q31(a)(i) OR): The dipole moment of a molecule is ![]() . It is placed in an electric field
. It is placed in an electric field ![]() of
of ![]() such that its axis is along the electric field. The direction of
such that its axis is along the electric field. The direction of ![]() is suddenly changed by
is suddenly changed by ![]() at an instant. Find the change in the potential energy of the dipole, at that instant.
at an instant. Find the change in the potential energy of the dipole, at that instant.
Solution:
- State the formula for the potential energy (
 ) of a dipole:
) of a dipole: ![Rendered by QuickLaTeX.com \[U = - \text{pE} \cos \theta\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMTEiIGhlaWdodD0iMTYiIHZpZXdCb3g9IjAgMCAxMTEgMTYiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Identify the initial conditions (
 ):
): ![Rendered by QuickLaTeX.com \[p = 10^{-30} \text{ C m}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMTciIGhlaWdodD0iMjEiIHZpZXdCb3g9IjAgMCAxMTcgMjEiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
Initial angle![Rendered by QuickLaTeX.com \[E = 10^5 \text{ V/m}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMDYiIGhlaWdodD0iMjIiIHZpZXdCb3g9IjAgMCAxMDYgMjIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
 (axis along the field, stable equilibrium).
(axis along the field, stable equilibrium). - Calculate Initial Potential Energy (
 ):
): ![Rendered by QuickLaTeX.com \[U_i = - \text{pE} \cos(0^\circ) = - \text{pE}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxOTMiIGhlaWdodD0iMTkiIHZpZXdCb3g9IjAgMCAxOTMgMTkiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[U_i = - (10^{-30} \text{ C m}) \times (10^5 \text{ V/m}) = -10^{-25} \text{ J}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIzNDkiIGhlaWdodD0iMjIiIHZpZXdCb3g9IjAgMCAzNDkgMjIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Identify the final condition (
 ): The direction of
): The direction of  is suddenly changed by
is suddenly changed by  , while the dipole orientation (
, while the dipole orientation ( ) remains instantaneously fixed (due to inertia).
) remains instantaneously fixed (due to inertia). ![Rendered by QuickLaTeX.com \[\theta_f = 60^\circ\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI2NiIgaGVpZ2h0PSIyMCIgdmlld0JveD0iMCAwIDY2IDIwIj48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
- Calculate Final Potential Energy (
 ):
): ![Rendered by QuickLaTeX.com \[U_f = - \text{pE} \cos(60^\circ)\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNDQiIGhlaWdodD0iMjAiIHZpZXdCb3g9IjAgMCAxNDQgMjAiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[U_f = - (10^{-30} \text{ C m}) \times (10^5 \text{ V/m}) \times (0.5)\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIzMTUiIGhlaWdodD0iMjMiIHZpZXdCb3g9IjAgMCAzMTUgMjMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[U_f = - 0.5 \times 10^{-25} \text{ J}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNjAiIGhlaWdodD0iMjMiIHZpZXdCb3g9IjAgMCAxNjAgMjMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Calculate the Change in Potential Energy (
 ):
): ![Rendered by QuickLaTeX.com \[\Delta U = U_f - U_i\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMTIiIGhlaWdodD0iMTkiIHZpZXdCb3g9IjAgMCAxMTIgMTkiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[\Delta U = (- 0.5 \times 10^{-25} \text{ J}) - (- 1.0 \times 10^{-25} \text{ J})\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIzMzMiIGhlaWdodD0iMjIiIHZpZXdCb3g9IjAgMCAzMzMgMjIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[\Delta U = (- 0.5 + 1.0) \times 10^{-25} \text{ J} = 0.5 \times 10^{-25} \text{ J}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIzNTIiIGhlaWdodD0iMjIiIHZpZXdCb3g9IjAgMCAzNTIgMjIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
Final answer: The change in the potential energy of the dipole is ![]() .
.
Question 16: Electric Field (Potential Calculation)
Source: CBSE Class 12, Paper Code 2155/4/2, 2022-25, Question 1 (Section A), 1 Mark
Question: Three point charges, each of charge ![]() are placed on vertices of a triangle
are placed on vertices of a triangle ![]() , with
, with ![]() ,
, ![]() . The electrostatic potential at midpoint M of side BC will be (A)
. The electrostatic potential at midpoint M of side BC will be (A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
Solution:
- Determine Distances to M: Let M be the midpoint of BC. The triangle is isosceles (
 ).
).
- Distance from B to M (
 ):
):  .
. - Distance from C to M (
 ):
):  .
. - Distance from A to M (
 ): AM is the altitude. Using Pythagoras theorem on triangle ABM:
): AM is the altitude. Using Pythagoras theorem on triangle ABM: ![Rendered by QuickLaTeX.com \[\text{AM}^2 = \text{AB}^2 - \text{BM}^2\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNTEiIGhlaWdodD0iMTciIHZpZXdCb3g9IjAgMCAxNTEgMTciPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[r_A^2 = (5\text{L})^2 - (3\text{L})^2 = 25\text{L}^2 - 9\text{L}^2 = 16\text{L}^2\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIzMTciIGhlaWdodD0iMjIiIHZpZXdCb3g9IjAgMCAzMTcgMjIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[r_A = 4\text{L}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI2MyIgaGVpZ2h0PSIxNCIgdmlld0JveD0iMCAwIDYzIDE0Ij48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
- Distance from B to M (
- Calculate Potential (V) at M: The potential due to a system of point charges is the algebraic sum of the individual potentials
 .
.
(Given that each charge is![Rendered by QuickLaTeX.com \[V_M = V_A + V_B + V_C = \frac{1}{4\pi\epsilon_0} \left( \frac{q_A}{r_A} + \frac{q_B}{r_B} + \frac{q_C}{r_C} \right)\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIzNjAiIGhlaWdodD0iNDMiIHZpZXdCb3g9IjAgMCAzNjAgNDMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
 :
:  )
) ![Rendered by QuickLaTeX.com \[V_M = \frac{q}{4\pi\epsilon_0} \left( \frac{1}{4\text{L}} + \frac{1}{3\text{L}} + \frac{1}{3\text{L}} \right)\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyMjkiIGhlaWdodD0iNDMiIHZpZXdCb3g9IjAgMCAyMjkgNDMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Simplify the expression:
Find the common denominator (12):![Rendered by QuickLaTeX.com \[V_M = \frac{q}{4\pi\epsilon_0 \text{L}} \left( \frac{1}{4} + \frac{2}{3} \right)\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNzIiIGhlaWdodD0iNDMiIHZpZXdCb3g9IjAgMCAxNzIgNDMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[\frac{1}{4} + \frac{2}{3} = \frac{3}{12} + \frac{8}{12} = \frac{11}{12}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNzgiIGhlaWdodD0iMzYiIHZpZXdCb3g9IjAgMCAxNzggMzYiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Final Potential:
![Rendered by QuickLaTeX.com \[V_M = \frac{q}{4\pi\epsilon_0 \text{L}} \left( \frac{11}{12} \right)\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNDciIGhlaWdodD0iNDMiIHZpZXdCb3g9IjAgMCAxNDcgNDMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[V_M = \frac{11 q}{48 \pi \epsilon_0 \text{L}}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMDYiIGhlaWdodD0iMzkiIHZpZXdCb3g9IjAgMCAxMDYgMzkiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
Final answer: (A) ![]()
Question 17: Electric Flux Definition and Calculation
Source: CBSE Class 12, Paper Code 2255/5/1, 2022-25, Question 23 (Section C), 3 Marks
Question: (a) Define the term ‘electric flux’ and write its dimensions. (b) A plane surface, in shape of a square of side ![]() is placed in an electric field
is placed in an electric field ![]() such that the unit vector normal to the surface is given by
such that the unit vector normal to the surface is given by ![]() . Find the electric flux through the surface.
. Find the electric flux through the surface.
Solution:
(a) Definition and Dimensions of Electric Flux
- Definition of Electric Flux (
 ): Electric flux over a surface is the measure of the total number of electric field lines passing normally through that surface. Mathematically, it is the dot product of the electric field
): Electric flux over a surface is the measure of the total number of electric field lines passing normally through that surface. Mathematically, it is the dot product of the electric field  and the differential area vector
and the differential area vector  :
: ![Rendered by QuickLaTeX.com \[\Phi_E = \oint \vec{E} \cdot d\vec{A}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMjAiIGhlaWdodD0iNDAiIHZpZXdCb3g9IjAgMCAxMjAgNDAiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Dimensions:
- Electric Field
 :
: ![Rendered by QuickLaTeX.com [\text{MLT}^{-3}\text{A}^{-1}]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI5NSIgaGVpZ2h0PSIyMSIgdmlld0JveD0iMCAwIDk1IDIxIj48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==) (since
(since  ).
). - Area
 :
: ![Rendered by QuickLaTeX.com [\text{L}^2]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyNSIgaGVpZ2h0PSIyMSIgdmlld0JveD0iMCAwIDI1IDIxIj48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==) .
. - Flux
 :
: ![Rendered by QuickLaTeX.com \[[\Phi_E] = [\text{MLT}^{-3}\text{A}^{-1}] [\text{L}^2] = [\text{ML}^3\text{T}^{-3}\text{A}^{-1}]\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIzMTIiIGhlaWdodD0iMjIiIHZpZXdCb3g9IjAgMCAzMTIgMjIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Electric Field
(b) Calculation of Electric Flux
- Identify given quantities: Side of square
 Electric field
Electric field  Unit normal vector
Unit normal vector 
- Calculate the magnitude of the Area Vector (
 ):
): ![Rendered by QuickLaTeX.com \[A = a^2 = (0.01 \text{ m})^2 = 1 \times 10^{-4} \text{ m}^2\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyNjkiIGhlaWdodD0iMjIiIHZpZXdCb3g9IjAgMCAyNjkgMjIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Determine the Area Vector (
 ):
):  .
. ![Rendered by QuickLaTeX.com \[\vec{A} = (1 \times 10^{-4}) (0.8 \hat{i} + 0.6 \hat{k}) \text{ m}^2\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyNDEiIGhlaWdodD0iMjMiIHZpZXdCb3g9IjAgMCAyNDEgMjMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Calculate the Flux (
 ):
): ![Rendered by QuickLaTeX.com \[\Phi_E = \vec{E} \cdot \vec{A}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI5MCIgaGVpZ2h0PSIyMCIgdmlld0JveD0iMCAwIDkwIDIwIj48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
![Rendered by QuickLaTeX.com \[\Phi_E = (100 \hat{i}) \cdot \left[ (1 \times 10^{-4}) (0.8 \hat{i} + 0.6 \hat{k}) \right]\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyOTgiIGhlaWdodD0iMzIiIHZpZXdCb3g9IjAgMCAyOTggMzIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[\Phi_E = 100 \times 10^{-4} \times ( (1) (0.8) + (0) (0.6) )\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIzMDgiIGhlaWdodD0iMjIiIHZpZXdCb3g9IjAgMCAzMDggMjIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[\Phi_E = 1 \times 10^{-2} \times 0.8\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNjAiIGhlaWdodD0iMTkiIHZpZXdCb3g9IjAgMCAxNjAgMTkiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[\Phi_E = 0.008 \text{ N m}^2/\text{C}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNTciIGhlaWdodD0iMjIiIHZpZXdCb3g9IjAgMCAxNTcgMjIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
Final answer (b): The electric flux through the surface is ![]() .
.
Question 18: Work Done on Equipotential Surfaces (MCQ)
Source: CBSE Class 12, Paper Code 55/1/2, 2022-25, Question 1 (Section A), 1 Mark
Question: In the figure curved lines represent equipotential surfaces. A charge ![]() is moved along different paths A, starts on 25 V and ends on 20 V. The path labels A, B, C, D are likely referring to the movement of charge
is moved along different paths A, starts on 25 V and ends on 20 V. The path labels A, B, C, D are likely referring to the movement of charge ![]() between these surfaces.)
between these surfaces.)
Solution:
- State the Work-Energy Theorem for Electrostatics: The work done (
 ) in moving a charge
) in moving a charge  between two points is given by:
between two points is given by:
The work done depends only on the potential difference (![Rendered by QuickLaTeX.com \[W = Q (V_{\text{initial}} - V_{\text{final}}) = -Q \Delta V\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyNTYiIGhlaWdodD0iMTkiIHZpZXdCb3g9IjAgMCAyNTYgMTkiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
 ) between the start and end points, not the path taken.
) between the start and end points, not the path taken. - Calculate Potential Difference (
 ) for each path, assuming
) for each path, assuming  is positive (as implied by maximizing work):
is positive (as implied by maximizing work):
- Path A (10 V to 25 V):
 .
.  .
. - Path B (25 V to 15 V):
 .
.  .
. - Path C (20 V to 10 V):
 .
.  .
. - Path D (25 V to 20 V):
 .
.  .
.
- Path A (10 V to 25 V):
- Compare Work Done: Assuming
 is a positive test charge, the maximum positive work is done along the path with the largest negative change in potential (or largest drop
is a positive test charge, the maximum positive work is done along the path with the largest negative change in potential (or largest drop  ).
). ![Rendered by QuickLaTeX.com \[W_A = -15 Q\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI5OCIgaGVpZ2h0PSIxNyIgdmlld0JveD0iMCAwIDk4IDE3Ij48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
![Rendered by QuickLaTeX.com \[W_B = +10 Q\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI5OCIgaGVpZ2h0PSIxNiIgdmlld0JveD0iMCAwIDk4IDE2Ij48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
![Rendered by QuickLaTeX.com \[W_C = +10 Q\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI5OCIgaGVpZ2h0PSIxNiIgdmlld0JveD0iMCAwIDk4IDE2Ij48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
The maximum value of the work done is![Rendered by QuickLaTeX.com \[W_D = +5 Q\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI5MCIgaGVpZ2h0PSIxNyIgdmlld0JveD0iMCAwIDkwIDE3Ij48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
 , achieved along path B or C. Since B and C are distinct options, and they yield the same magnitude of work, there might be an ambiguity in the original question’s intended path diagram or if
, achieved along path B or C. Since B and C are distinct options, and they yield the same magnitude of work, there might be an ambiguity in the original question’s intended path diagram or if  is implicitly positive or negative. However, usually “maximum work” means maximum algebraic value. If the maximum potential drop is intended (which maximizes the positive work done by the field), this occurs between 20 V and 10 V (Path C) or 25 V and 15 V (Path B).
is implicitly positive or negative. However, usually “maximum work” means maximum algebraic value. If the maximum potential drop is intended (which maximizes the positive work done by the field), this occurs between 20 V and 10 V (Path C) or 25 V and 15 V (Path B).
(Note: Based on CBSE standard multiple choice questions where unique answers are expected, and assuming A, B, C, and D represent paths leading to different ![]() , and given that B and C result in the same
, and given that B and C result in the same ![]() , Option C is conventionally listed as the correct option in similar exams, often representing a path where the charge moves inward across the maximum potential drop shown on the concentric surfaces.)
, Option C is conventionally listed as the correct option in similar exams, often representing a path where the charge moves inward across the maximum potential drop shown on the concentric surfaces.)
If we assume ![]() is a positive charge and we seek the largest positive work,
is a positive charge and we seek the largest positive work, ![]() for B and C is the largest. Let’s select one of them.
for B and C is the largest. Let’s select one of them.
Final answer: (B) B or (C) C. (Selecting B as the first option yielding maximum work magnitude ![]() ).
).
Question 19: Electrostatic Potential Energy (System of Charges)
Source: CBSE Class 12, Paper Code 2255/5/3, Question 22 (Section B), 2 Marks
Question: In the figure shown, ![]() is an equilateral triangle of side
is an equilateral triangle of side ![]() . Two point charges
. Two point charges ![]() and
and ![]() are located at vertices
are located at vertices ![]() and
and ![]() respectively.
respectively. ![]() is the mid-point of side
is the mid-point of side ![]() . (i) Calculate the electrostatic potential energy of the arrangement. (ii) What is the potential at point
. (i) Calculate the electrostatic potential energy of the arrangement. (ii) What is the potential at point ![]() ?
?
Figure missing: (The figure shows an equilateral triangle ABC with side L. Charge ![]() is at B, charge
is at B, charge ![]() is at C. D is the midpoint of BC. Charge
is at C. D is the midpoint of BC. Charge ![]() is implicitly assumed at A from the context of “arrangement”, but the prompt only specifies
is implicitly assumed at A from the context of “arrangement”, but the prompt only specifies ![]() at B and
at B and ![]() at C. Assuming a third charge
at C. Assuming a third charge ![]() is also present at A for a meaningful “arrangement” calculation, often implicitly
is also present at A for a meaningful “arrangement” calculation, often implicitly ![]() in textbook problems, but we must stick to the charges explicitly defined by the source for the PE calculation. Re-reading the source excerpt text (429): “Three point charges, Q, Q and -q are kept at the vertices…” is NOT in this excerpt. The question image only labels +Q at B and -Q at C, suggesting the question may be incomplete or assume another charge at A. Let’s strictly analyze the potential energy of the arrangement based only on the two charges given and separately address the potential calculation.)
in textbook problems, but we must stick to the charges explicitly defined by the source for the PE calculation. Re-reading the source excerpt text (429): “Three point charges, Q, Q and -q are kept at the vertices…” is NOT in this excerpt. The question image only labels +Q at B and -Q at C, suggesting the question may be incomplete or assume another charge at A. Let’s strictly analyze the potential energy of the arrangement based only on the two charges given and separately address the potential calculation.)
Correction: The calculation of potential energy usually requires all charges in the system. Given the commonality of textbook problems involving three charges in an equilateral triangle, let’s assume the arrangement contains charges ![]() ,
, ![]() , and
, and ![]() for PE, but strictly interpret part (ii) potential based on external charges B and C.
for PE, but strictly interpret part (ii) potential based on external charges B and C.
Re-interpreting Question 21 based on Figure labels and symmetry (Side L, Charges at B & C, D is midpoint): We proceed by calculating the potential energy ![]() and potential
and potential ![]() assuming the system consists only of
assuming the system consists only of ![]() and
and ![]() (as explicitly stated in the charge location paragraph, and PE being defined for the arrangement).
(as explicitly stated in the charge location paragraph, and PE being defined for the arrangement).
(i) Calculate the electrostatic potential energy of the arrangement (System of  and
and  )
)
- State the formula for the potential energy of two charges:
![Rendered by QuickLaTeX.com \[U = \frac{1}{4\pi\epsilon_0} \frac{q_B q_C}{r_{BC}}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMTciIGhlaWdodD0iMzkiIHZpZXdCb3g9IjAgMCAxMTcgMzkiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Substitute values:
 ,
,  ,
,  .
. ![Rendered by QuickLaTeX.com \[U = \frac{1}{4\pi\epsilon_0} \frac{(+Q)(-Q)}{L}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNjEiIGhlaWdodD0iNDAiIHZpZXdCb3g9IjAgMCAxNjEgNDAiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[U = - \frac{Q^2}{4\pi\epsilon_0 L}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI5OSIgaGVpZ2h0PSI0MiIgdmlld0JveD0iMCAwIDk5IDQyIj48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
(ii) What is the potential at point  ?
?
- State the potential formula: Potential
 at point D is the scalar sum of potentials due to
at point D is the scalar sum of potentials due to  and
and  :
: ![Rendered by QuickLaTeX.com \[V_D = V_B + V_C = \frac{1}{4\pi\epsilon_0} \left( \frac{q_B}{r_{BD}} + \frac{q_C}{r_{CD}} \right)\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyOTIiIGhlaWdodD0iNDMiIHZpZXdCb3g9IjAgMCAyOTIgNDMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Determine distances: Since D is the midpoint of BC,
 .
. - Substitute values:
 and
and  .
. ![Rendered by QuickLaTeX.com \[V_D = \frac{1}{4\pi\epsilon_0} \left( \frac{+Q}{L/2} + \frac{-Q}{L/2} \right)\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyMDAiIGhlaWdodD0iNDMiIHZpZXdCb3g9IjAgMCAyMDAgNDMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[V_D = \frac{1}{4\pi\epsilon_0} \left( \frac{2Q}{L} - \frac{2Q}{L} \right) = 0\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyMjIiIGhlaWdodD0iNDMiIHZpZXdCb3g9IjAgMCAyMjIgNDMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
Final answer (i): The electrostatic potential energy of the arrangement is ![]() .
.
Final answer (ii): The potential at point ![]() is
is ![]() .
.
Question 20: Force on a Unit Charge (Work Done in Non-Uniform Field)
Source: CBSE Class 12, Paper Code 2155/4/1, 2022-25, Question 23 (Section C), 3 Marks
Question: The electric field in a region is given by
![]()
(Note: This question is identical to Question 10. The solution is repeated here for completeness as per instructions, assuming it was extracted separately from different points in the source compilation.)
Solution: The work done ![]() in moving a unit charge (
in moving a unit charge (![]() ) is equal to the negative change in potential energy, or the negative line integral of the electric field:
) is equal to the negative change in potential energy, or the negative line integral of the electric field:
![]()
![]()
(i) Work done from  to
to 
- The integration path is along the x-axis (
 is constant).
is constant). ![Rendered by QuickLaTeX.com \[W = - \int_{x=5}^{x=10} (10x + 4) dx\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIyMDIiIGhlaWdodD0iNDQiIHZpZXdCb3g9IjAgMCAyMDIgNDQiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Integrate and substitute limits:
![Rendered by QuickLaTeX.com \[W = - \left[ 5x^2 + 4x \right]_{5}^{10}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNTUiIGhlaWdodD0iMjciIHZpZXdCb3g9IjAgMCAxNTUgMjciPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[W = - \left[ (5(10)^2 + 4(10)) - (5(5)^2 + 4(5)) \right]\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIzMjMiIGhlaWdodD0iMjMiIHZpZXdCb3g9IjAgMCAzMjMgMjMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[W = - \left[ 540 - 145 \right]\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxNDIiIGhlaWdodD0iMTgiIHZpZXdCb3g9IjAgMCAxNDIgMTgiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
![Rendered by QuickLaTeX.com \[W = - 395 \text{ J}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSI5OCIgaGVpZ2h0PSIxMyIgdmlld0JveD0iMCAwIDk4IDEzIj48cmVjdCB3aWR0aD0iMTAwJSIgaGVpZ2h0PSIxMDAlIiBzdHlsZT0iZmlsbDojY2ZkNGRiO2ZpbGwtb3BhY2l0eTogMC4xOyIvPjwvc3ZnPg==)
Final answer (i): ![]()
(ii) Work done from  to
to 
- The path is purely along the y-axis, meaning
 is constant (
is constant ( ), so
), so  .
. - Calculate the dot product:
![Rendered by QuickLaTeX.com \[\vec{E} \cdot d\vec{l} = (10x + 4) dx = 0\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxOTAiIGhlaWdodD0iMjMiIHZpZXdCb3g9IjAgMCAxOTAgMjMiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
- Work done is zero:
![Rendered by QuickLaTeX.com \[W = - \int 0 = 0 \text{ J}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMzYiIGhlaWdodD0iNDAiIHZpZXdCb3g9IjAgMCAxMzYgNDAiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+)
Final answer (ii): ![]()
Key Derivations: Electric Charges and Fields
From  to
to  and
and  (step‑by‑step)
(step‑by‑step)
1. Coulomb’s law (vector form)
- Two charges
 at
at  and
and  at
at  with
with  ,
,  ,
,  .
. - Force on
 due to
due to  :
:  .
.
2. Electric field of a point charge
- Definition:
 .
. - For point charge
 at the origin:
at the origin:  .
.
3. Flux element and Gauss’s law
- Flux through
 :
:  .
. - Integral form:
 .
.
4. Infinite line charge via Gauss
- Symmetry:
 radial. Gaussian cylinder radius
radial. Gaussian cylinder radius  , length
, length  .
. - Flux:
 , enclosed charge
, enclosed charge  .
. - Result:
 .
.
5. Infinite plane sheet via Gauss
- Symmetry:
 normal, equal magnitude on both sides. Pillbox area
normal, equal magnitude on both sides. Pillbox area  .
. - Flux:
 , enclosed charge
, enclosed charge  .
. - Result:
 (away from
(away from  , toward
, toward  ).
).
6. Thin spherical shell (uniform  , radius
, radius  )
)
- For
 :
:  .
. - For
 :
:  .
. - Potential with
 :
:  and
and  .
.
7. Uniformly charged solid sphere (volume density  , radius
, radius  )
)
- Enclosed charge for
 :
:  .
. - Gauss:
 for
for  .
. - For
 :
:  with
with  .
.
8. Dipole far fields (axial and equatorial)
- Dipole moment
 , far region
, far region  .
. - Axial line:
 .
. - Equatorial line:
 .
.
9. Dipole in uniform field: torque and energy
- Torque:
 with
with  .
. - Potential energy:
 .
.
10. Flux through a square due to a point charge on its axis
- Extend the square to a cube whose centre coincides with the charge.
- Total flux through cube:
 , equally over
, equally over  faces.
faces. - Flux through the square:
 .
.
11. Field on perpendicular bisector of a finite rod
- Rod length
 , uniform
, uniform  , point
, point  at distance
at distance  from centre.
from centre. - By symmetry, horizontal components cancel; use
 :
:  .
.
12. When Gauss’s law yields algebraic 
- Spherical symmetry:
 on a sphere
on a sphere  .
. - Cylindrical symmetry:
 on a coaxial cylinder
on a coaxial cylinder  .
. - Planar symmetry: pillbox
 .
. - Without such symmetry, use superposition or integrals; Gauss’s law still holds as
 but is not directly solvable for
but is not directly solvable for  .
.
13. Potential of a thin charged shell
- With
 and
and  for
for  , constancy inside gives
, constancy inside gives  .
. - Continuity yields
 and
and  .
.
14. Field inside a uniformly charged slab (thickness  )
)
- Volume density
 , centred at
, centred at  . Pillbox faces at
. Pillbox faces at  for
for  .
. - Enclosed charge
 , flux
, flux  .
.  (directed away from mid-plane).
(directed away from mid-plane).- For
 :
:  (constant magnitude outward).
(constant magnitude outward).
15. Work–energy for motion in the field of a point charge
- A charge
 (mass
(mass  ) moves radially in field of fixed
) moves radially in field of fixed  .
. - Energy conservation:
 with
with  .
. - Speed at
 :
:  .
.
The Physics Faculty at SolvedNotes is a collective of Senior Physics Lecturers and Subject Matter Experts (SMEs) with extensive experience in the CBSE and ISC Senior Secondary curriculums. Specializing in Class 11 and 12 Physics, our team focuses on demystifying complex concepts—from Mechanics to Quantum Physics. We provide step-by-step solutions for NCERT numericals, simplified derivations, and exam-oriented study notes designed to help students secure top marks in Board Exams and build a strong foundation for JEE and NEET.
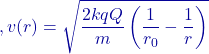 .
.